今回は画像の幾何学的変換の入門的な部分であるを画像の線形変換の基礎的な事項を中心に説明します!
画像をピクセルごとの数値の行列を羅列していると考えた場合、簡単な線形代数を適用して一次変換処理が行えます。
行列演算が可能ということは、移動・回転・拡大・縮小・鏡面変換・合成変換などの線形変換による単純な一次変換から、固有値や固有ベクトルなどの特徴量計算まで、多彩な処理が可能となります。
画像変換処理と行列演算
まず、ベクトル・行列演算を復習していきます。
はじめに次の図をご参照ください。
例えば 画像間演算などで、2つの画像を足し算する場合は、単に個々のピクセル同士の足し算になります。
これは画像も行列も同じであり、上図に示した行列の和と同じ処理です。
線形変換では主に行列やベクトルの積としての考え方が基本で、図のベクトルの積および行列の積のような計算が使用されます。
ベクトルの積は、この例ですと、
(1・4)+(2・5)+(3・6) = 32
行列の積は、
1・4+4・5+7・6 = 66
(繰り返し)
(図の引用:http://www.geisya.or.jp/~mwm48961/kou2/matrix2.html)
線形変換であるがゆえに、基本は高校の授業で習ったような一次変換です。
一次変換の基本式を次に示します。
ImageJを用いた機何変換処理
1.画像の拡大と縮小
二次元画像のx成分とy成分を独立して拡大縮小する場合の処理方法を示します。
画像をX軸方向にSx、Y軸方向にSy、だけ拡大縮小する処理は以下のとおりです。
次の図は、オリジナル画像を二倍拡大する処理の例です。ImageJでは、Image>Scaleでスケール値を2.0(2倍拡大)や0.5(1/2縮小)などの操作ができます。Image>Zoomや、ImageJメインメニュー内の虫眼鏡マークのクリック操作でも同じような処理が可能です。
(オリジナル画像とScale設定ウィンドウ)
(0.5倍に縮小、マトリクス数も半分に)
2.回転
原点を中心に、反時計回りに角度θだけ回転する変換式は次の通りです。
ImageJでの操作方法は、Image>Transform>Rotateで、角度θ(ここでは45)の入力をします。
3.鏡映
鏡映とは、ある任意の軸を空間軸に設定し、その軸に対象に画像を折り返す変換です。
X軸を基準にして折り返す変換は次のように表されます。
Y時の場合は次のようになります。
操作はImage>Transformで、Flip Horizontally(X軸基準鏡映:左右反転)、Flip Vertically(Y軸基準鏡映:上下反転)などの操作ができます。
(左右反転例)
4.スキュー
矩形画像を平行四辺形に変形するような変換を「スキュー」「せん断変換」といいます。
X軸方向へせん断する場合の変換式は次のようになります。
このうち、bは傾ける角度をθとすると、b=tanθとなります。
Y軸方向へのせん断は次のようになります。
ImageJでの操作は、Meijering氏が作成したTransformJを用います。
(http://imagescience.org/meijering/software/transformj/)
2015/9時点では、このプラグインはver1.5以上でないと動作しないというメッセージがでますので、Fijiという次世代のImageJを使って操作した例を示します。
Fijiには、デフォルトでこのプラグインが入っていますので、そのままPluginsからTransform>TransformJを選択して、Affineを使ってみます。
Affineを起動すると、1次変換のマトリクスをロードして、実行するウィンドウが表示されます。
はじめて起動するときには、このマトリクスファイルが作られていないので、新しく作成(create)してみます。createを起動すると、マトリクスが入力できるウィンドウが表示されます。ここでは、斜めに変換するような1次変換を行ってみます。
これをSaveして、先のウィンドウにロードして実行すると、次のようになります。
以上、今回は普段何気なく使っている機能の幾何変換処理を説明しました。
次回も続けて画像の幾何変換について説明します!
Reference
- 「山本修司:ImageJで学ぶ実践医用・バイオ画像処理.INNERVISION(21・7) 2006, p102-103」






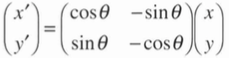











0 件のコメント:
コメントを投稿